こんにちは。グラフィックファシリテーター®やまざきゆにこです。

【NRIプレゼンツ☆知っておきたいデータサイエンス用語】

野村総研　未来創発センター「データサイエンスラボ」さまの新しい取り組み　NRI「データサイエンス用語」の解説動画（絵巻物）第１１弾がYouTubeアップされました。今回は（2分で解説しきれなかった！）「回帰分析におけるｔ値とｐ値」です。

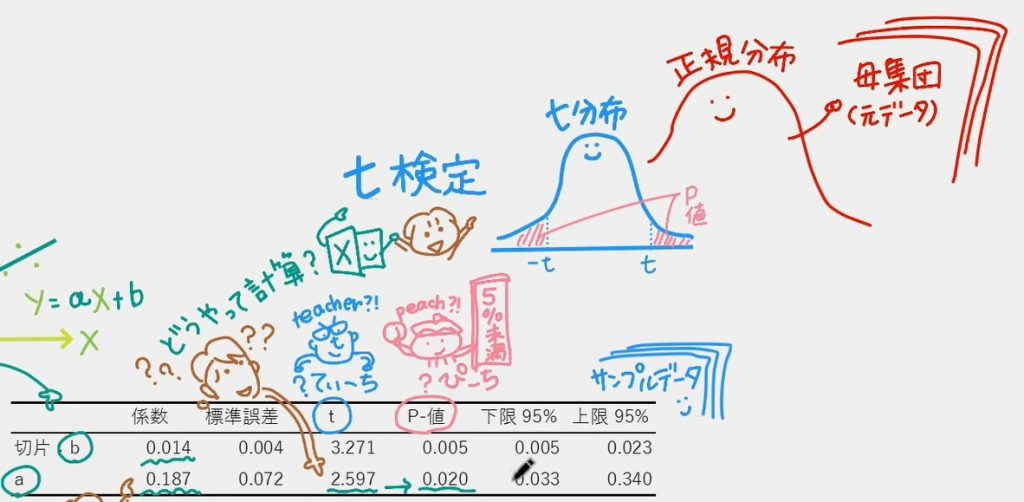
「ｐ値＜５％未満ならオッケー」でもいいけれど、今回は２つの数字が「そもそもｐ値がどうやって計算されて算出されているか」知らずに使ってない？「そもそもｐ値は、ｔ値が計算されて出てくるんだよ」ちゃんと知っておきましょうね、という動画です。

といっても、そもそもわたしは「てぃ～ちとぴ～ち？？？」「Excelにこんな機能があったの？！」

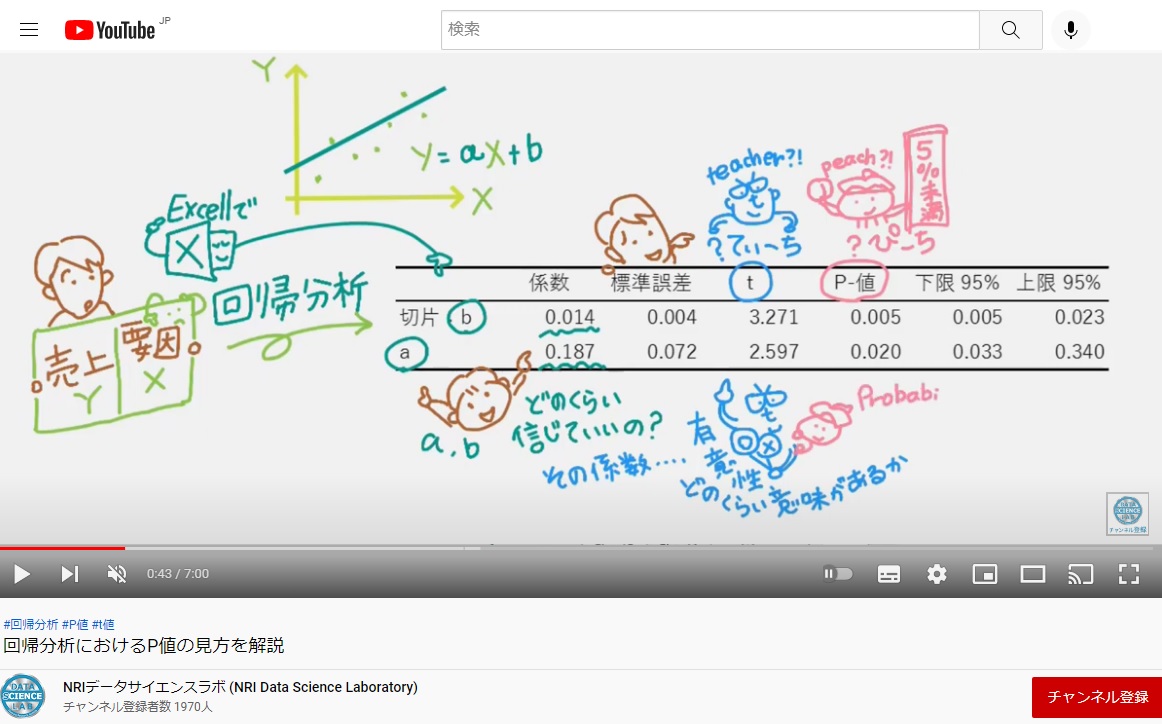
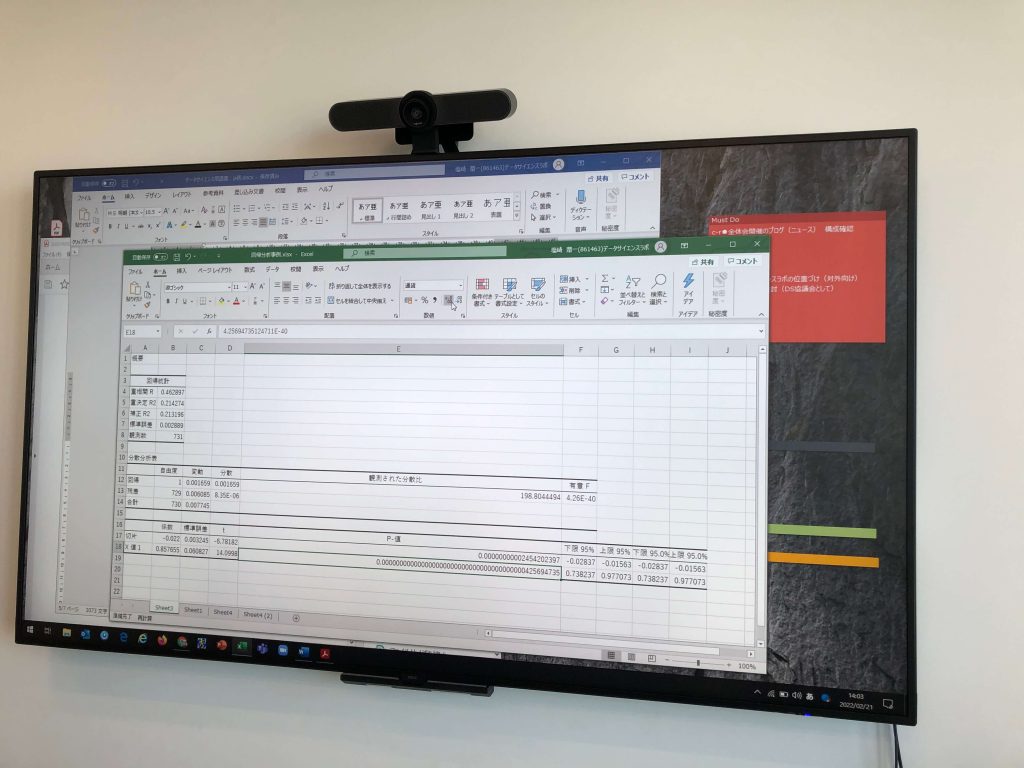
「回帰分析」というボタンを押せば、Y＝ａ＊X＋ｂの係数ａとｂを計算してくれちゃうなんてことすら知らなかったので、イントロではそんなじぶんのために、Excel画面をわざわざ作って動画にしました。「回帰分析」というボタンを押した結果が、Excelの２枚目のシートに出てくるのが「ｔ値」と「ｐ値」。

↓動画はこちら

↓用語解説「Ｐ値（P Value）とは」はこちらhttps://www.nri.com/jp/knowledge/glossary/lst/alphabet/p_value

一般的には、「ｐ値」さえ見ればいいと思っている人が多いそうです。「ｐ値が５％未満ならａとｂは間違ってない」とか「５％以上だからそもそもサンプルの抽出の仕方が間違ってるとか」。でも実は主役は「ｔ値」。「ｔ値」が算出された結果「ｐ値」が自動的に決まるそう。「ｔ値は何を意味していて、どうやって計算された結果なのか」知っておきましょうという解説動画になっています。

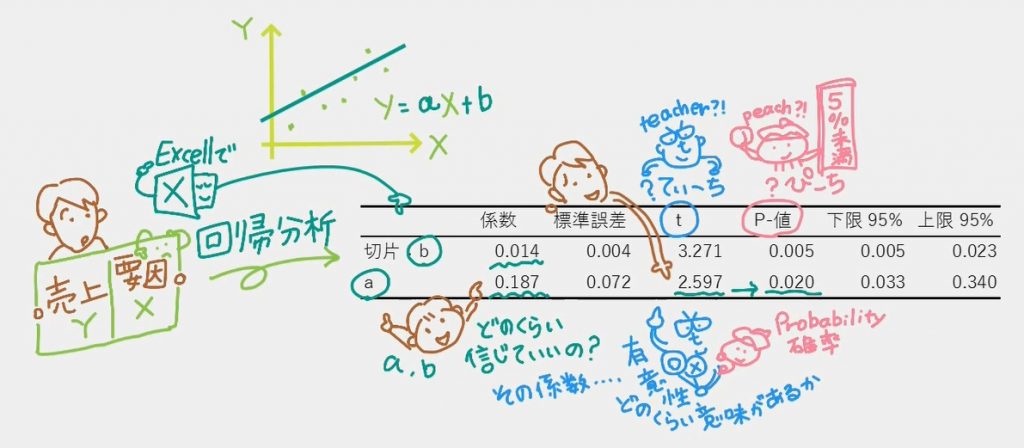
しかし、、、わたしにとっては聞きなれない「ｔ値」と「ｐ値」…。NRIのデータサイエンティストのＳさんが「ｔ値」と「ｐ値」を連呼するたびに、わたしには「てぃーち？＝teach？」「ぴーち？＝peach＝桃？！」としか聞こえず、結局、動画の中には「鼻の形がｔになった先生teacher」と「桃peachを手にした桃太郎PeachJohn」が最初から最後まで登場することに。。。探してみてください。

動画のポイントは以下↓静止画で、わたしのメモとあわせて、ぜひ押さえてください♪

今回は９つの章に分けて制作しました。↓この９つのキーワードで追いかけてもらえると理解が深まるのでは。

01「Excelで回帰分析をする」ときに必ず出てくる「ｔ値とｐ値」

↓06「ｔ検定」を理解するための　02～05
02「正規分布」
03「標準偏差」母集団のバラツキ
04「標準誤差」サンプルデータのバラツキ
05「ｔ分布」正規分布と似てる

06「ｔ検定」仮説検定の１つ
07「ｔ値とｐ値」

08　ようやく「回帰分析」の話に戻って「ｔ検定」
09　さいごに「サンプル数」が増えると注意！

01　「Excelで回帰分析をする」ときに必ず出てくる「ｔ値とｐ値」

まずはイントロでビジネスでのあるあるシーンを紹介していますが、この後いったん（02~07まで）「Excelで回帰分析」のシチュエーションから離れます。忘れた頃に(08で）戻ってきます。

「ｔ値」とは：「ｔ分布」を使って、仮説（その係数は正しいの？データの抽出はあってるの？）を検定する「ｔ検定」をしたときに出てくる数値ということなのですが、、、「ｔ検定」の前に「ｔ分布」を理解しないと始まらない。そのためには基本の「正規分布」をまずは理解しましょうねというのが次のパートです。

02　「正規分布」

ここで、そもそもですね、分析やデータの扱い方のシロウトは、母集団（元データ）とサンプルデータの概念がなかったので、最初いくら話を聞いても混乱してました。

「大きな母集団＝日本人の人口を調べるのは無理だよね」だから「抽出したサンプルデータから推計するんだよ」という、データ分析している人たちにとっては当たり前の概念。

母集団（元データ）の話をしているのか、サンプルデータの話をしているのか、綺麗に分けて考えないと混乱するので、まずは「母集団で正規分布と標準偏差」の話をする動画を先に描きました。

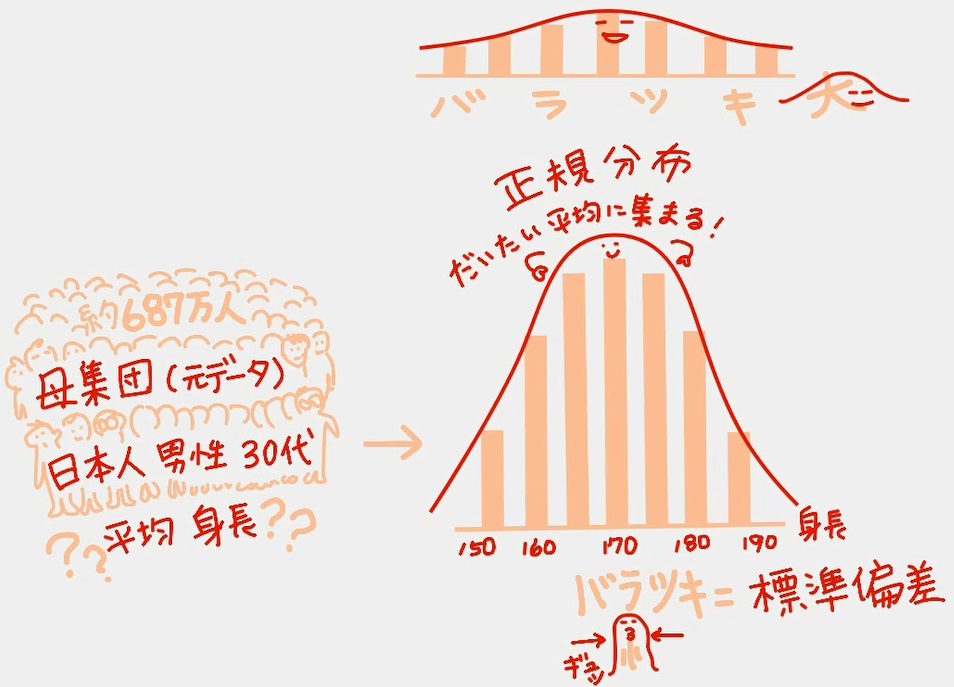
・身長などのデータ（母集団元データ）は「正規分布」になる。
・データはだいたい平均に集まる。
・データのバラツキが大きい場合には、裾野が広い形になる。
・データのバラツキが小さい場合には、裾野が狭い形になる。（動画には「ぎゅッ」と描いてます）
・このバラツキを「標準偏差」と呼ぶ。

参考：バラツキ「標準偏差」って？
「100点満点中70点とった」「10人の平均点は60点だった」で喜んでいいのかどうか。が、このバラツキ「標準偏差」で分かるということ。①「バラツキ＝大」の場合：ほとんどが高得点をとっていて（６人以上が70点～95点）、一部の人が平均点を下げていた（３人が０～10点）ので、「平均点70点とった私」は「下から４番目」だった！②「バラツキ＝小」の場合：ほとんどが60点以下で（８人が50点~60点）一部の人が高得点（２人が70点代）だったので、「平均点70点とった私」は「上から２番目」だった！

03　「標準偏差」母集団のバラツキ

正規分布に従うデータの場合は、平均の周辺に、どのぐらいの確率で、データが集まるのかがわかってるのだそう。

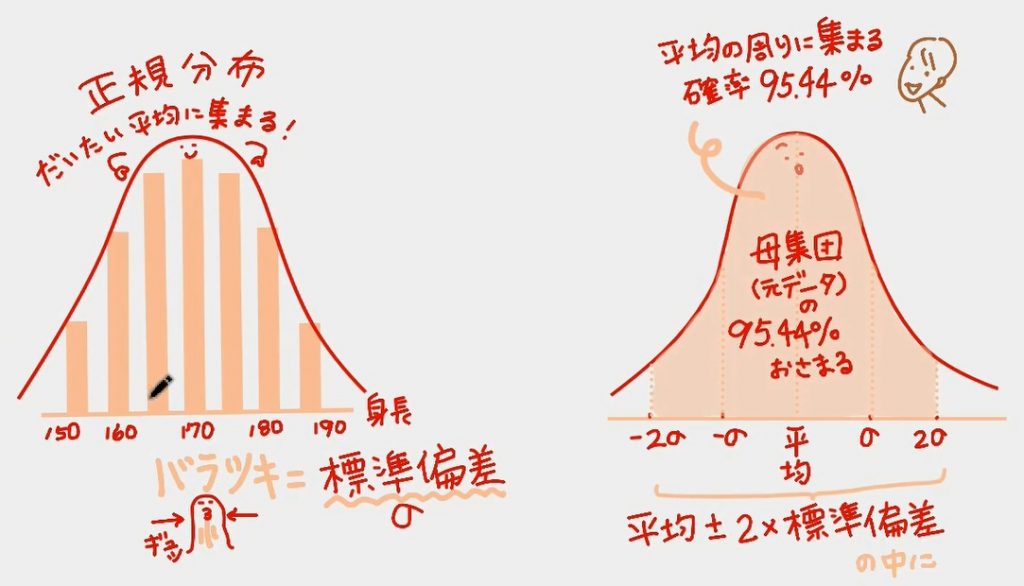
・平均±標準偏差　の範囲にあるデータは68.26%
・平均±2*標準偏差　の範囲にあるデータは95.44%
・平均±3*標準偏差　の範囲にあるデータは99.74%

動画ではこの後「ｔ値」の話で「95％」がカギになるので、それにつながる「２×標準偏差」を残しています。

04　「標準誤差」サンプルデータのバラツキ

ここからは「母集団（元データ）」ではなく「サンプルデータ」の話に移ります。「母集団（元データ）」を計算することはできないので、「サンプルデータ」を使うわけですが、母集団での考え方と同じように「サンプルデータ」を使って計算したときのバラツキは「標準誤差」と呼びますよというのがこの動画。

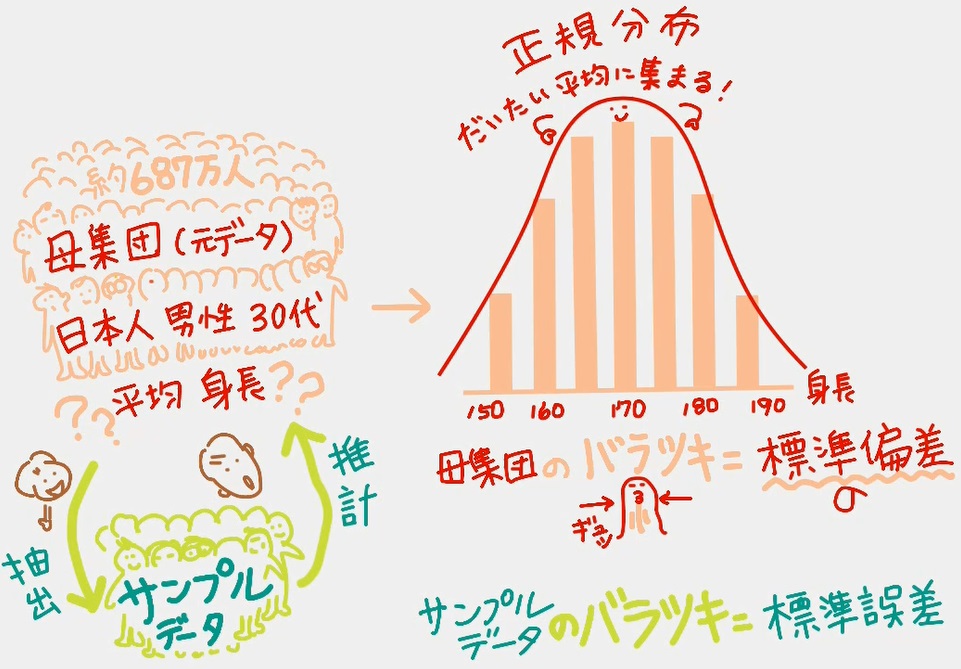
（なぜ誤差という言葉に変わるのか分かりませんが、母集団で計算して出るはずの正確な標準偏差の数値よりは誤差があるよねってことですかね）

・95.44%の確率で　サンプルデータの平均値±2×標準誤差 の範囲におさまる

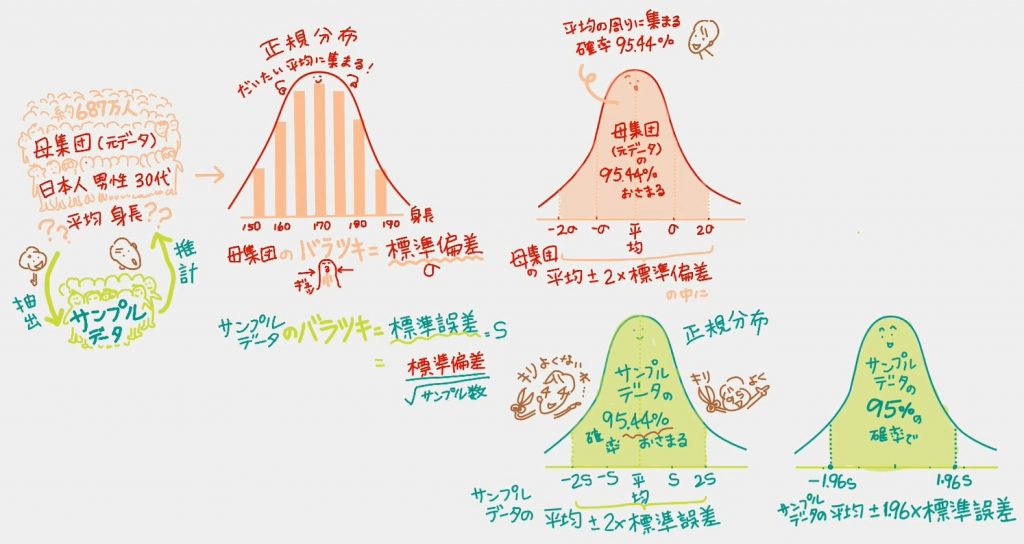
そして、ここからちょっと面白いというか人間味がある話なんですけど「95.44％の確率って、なんだかキリがよくないね。95%の確率で考えよう」ってことになって

・95%の確率で　170±1.96*標準誤差　の範囲におさまる

としちゃうんです。ただ、ここまで説明されて「おいおい」という展開になります！！！

「理論上ではこうなんだけど、実質モンダイ無理なんだよね。なぜって、標準誤差ってさ、こういう計算式で出てくるんだけど

・サンプルデータの標準誤差　＝　元データの標準偏差　／　√サンプル数

『元データの標準偏差』が分からないから、標準誤差も分からないんだよね」と。

「……(-_-)」？？？

ここでさらなる「！！！」。ウラ技（？）が繰り出されます！！！

05　「ｔ分布」正規分布と似てる

「『元データの標準偏差』は分からないから、『サンプルデータ』から標準偏差を求めて、それで代替しちゃおう！」

「え？そんなんでいいの？！」って感じですけど話は進みます。

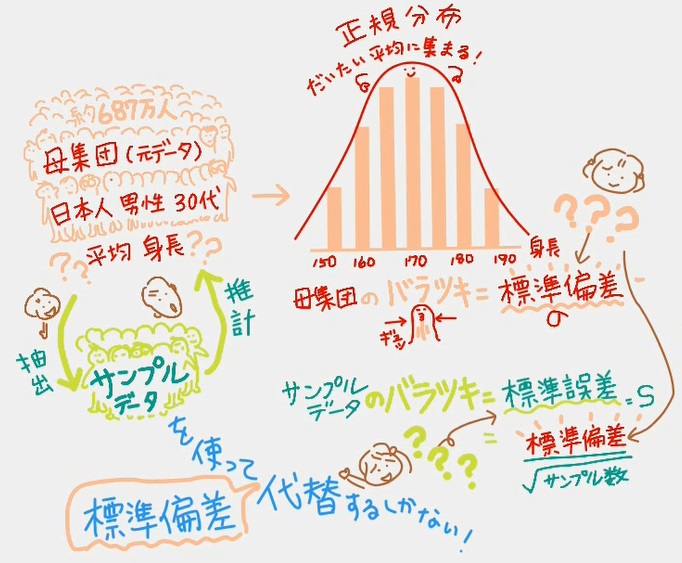
ここで計算された結果はもはや「正規分布」にはならない。
正規分布に似ている（少しだけ裾野が広い）「ｔ分布」に従う。

・サンプルデータの数で形が異なる「ｔ分布」。
・「サンプルデータの数―１＝自由度」ごとに「ｔ分布」が描ける。
・「サンプルデータの数が増える＝自由度が大きな値をとる」と正規分布に近くなる

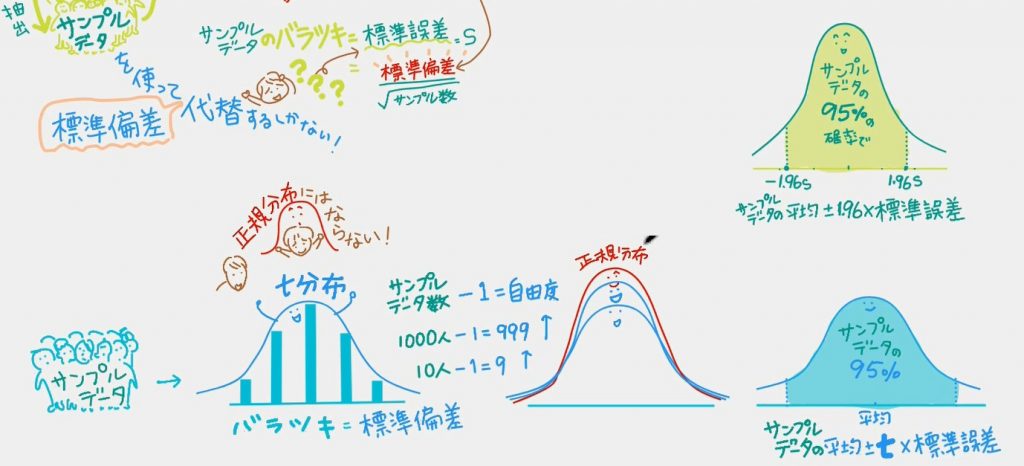
・95%の確率で　170±ｔ*標準誤差　の範囲におさまる

で、ここでようやく「ｔ」の文字が出てきましたが、そもそも「ｔ値」とは：「ｔ分布」を使って、仮説（その係数は正しいの？データの抽出はあってるの？）を検定する「ｔ検定」をしたときに出てくる数値。ということで、。「ｔ検定」の話をしたくて、でもその前に「ｔ分布」を理解しないと始まらないので、「正規分布」からここまで解説してきました。ふぅ～長かった。ようやく「ｔ検定」です。

06　「ｔ検定」仮説検定の１つ

しかし「ｔ検定」とは「ｔ分布」を使って「仮説として用いた値が正しいかどうか」を確かめること、、、と言われても「？？？」だったわたし。よくよく聞くと、もともと「仮説検定」という考え方があって、そのうちの１つに「ｔ検定」という検定法があるのだそう。

この説明の順番が分かり易かったので動画の中でも、そもそも「仮説検定」って何？を解説しています。

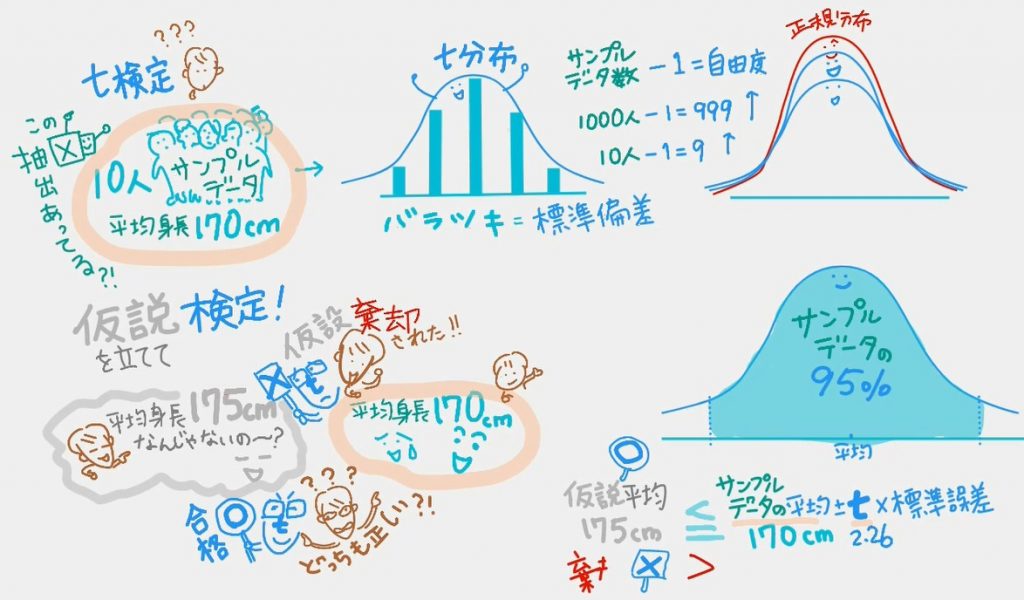
ちなみに「仮説検定」＝「仮説としておいた数字が正しいかどうかを検定する」という説明を聞いたら、それほど混乱しないんですけど、じつは「仮説が棄却されると嬉しい」というのがポイントです。ここ、要注意。

「仮説が正しい」と嬉しくない。
「仮説が棄却される」と嬉しい。ってどゆこと？

動画では「今回抽出したサンプルデータの平均は170でした」と出たけど、もしかしたら「平均175なんじゃないの？」という（できれば棄却できそうな）仮説をぶつけて、「今回抽出したサンプルデータの平均は170でした」が正しそうかどうかを検定しています。

なぜ棄却されると嬉しいかと言うと、もし「平均175なんじゃないの？」という仮説が「正しい」と出ちゃうと、「あれ？平均は170も正しそうだし、平均175も正しいそう」という「どっちも正しそう」となって結論が出ない。理想は「平均175はありえない！」と棄却されたほうが「平均は170は正しそうだね、ホッ」となって一件落着なわけです。

07　「ｔ値とｐ値」

「ｔ値」は以下のように定義して、これを「検定統計量」と呼ぶ。

－（サンプル平均値－仮説平均値）÷（サンプル標準誤差）
≦　t　≦＋（サンプル平均値－仮説平均値）÷（サンプル標準誤差）
　　　↓
ｔ値＝±（サンプル平均値－仮説平均値）÷（サンプル標準誤差）

「ｔ値」より外側になる確率のことを「ｐ値」と言います。

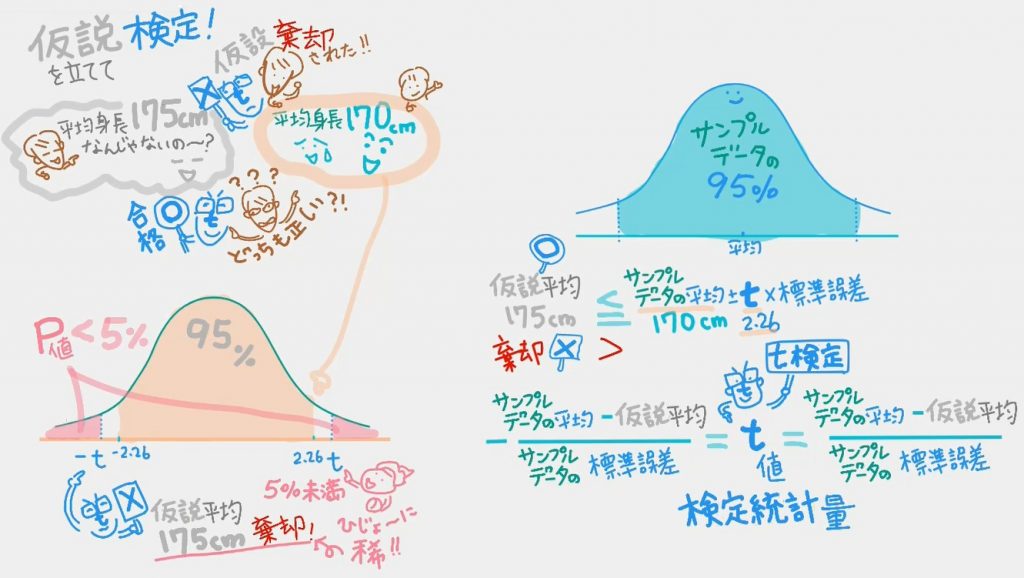
「ｔ分布」の横軸に「ｔ値」をプロットしたとき、「確率95％の中におさまらない」なら、95％より外側＝起こり得るのは確率「ｐ値」は５％未満＝滅多にありえない＝棄却！となります。

08　ようやく「回帰分析」の話に戻って「ｔ検定」

回帰分析の結果Y＝ａ＊X＋ｂに「ｔ検定」を行い、回帰係数であるａの確からしさを検定しているというワケ。

ｔ値＝（サンプル平均値－仮説平均値）÷（サンプル標準誤差）
　　＝（計算されたａ－ａの仮説）÷（ａの標準誤差）

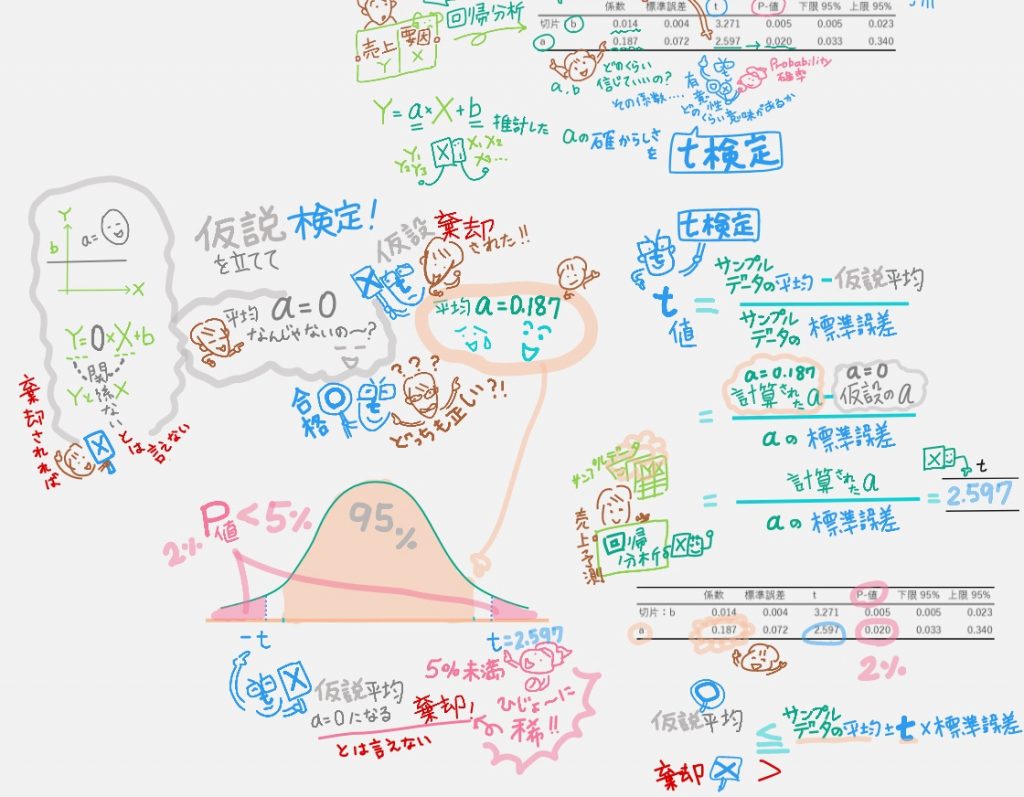
ここで「ａ＝ゼロ」というありえない仮説を立てます。(棄却したい）

ｔ値＝（計算されたa－0）÷（aの標準誤差）
　　＝（計算されたa）÷（aの標準誤差）

Excelの回帰分析結果の「ｔ」は、この式で計算されたものなのです。

09　さいごに「サンプル数」が増えると注意！

とはいえ、このｔやｐの数値結果を鵜呑みに信じないでね、という最近話題の話で動画のさいごをしめくくっています。最近ビッグデータを扱えるようになっていますが、じつはこのｔの計算式をよく見ると…

つまり「サンプル数」が大きくなるほど、「ｔ値」は大きくなる。すると「ｐ値」は小さくなる。つまり「ａ＝0」という仮説が棄却されやすくなる＝回帰分析が正しいという判断がされやすくなってしまう。

ビッグデータが扱えるようになって、古く注目されてもこなかった統計学の理論が脚光を浴びる一方で、こんなふうに通用しなくなる状況も生まれてきたり。データサイエンスの面白いところでもありますね。

【動画制作ウラ話】

前回に引き続き、今回も、わたしの手書きメモのほんの一部をこちらにアップしておきます。自分を労うために記念として記録を残したいだけですが(^^ゞ

最初にＮＲＩのデータサイエンティストさんにレクチャーを２時間ほど受けるのですが、１回で理解できることはまず稀でして。。。今回も所長自らここまで丁寧にサンプルデータを創って準備してくださって説明してくださっているのに

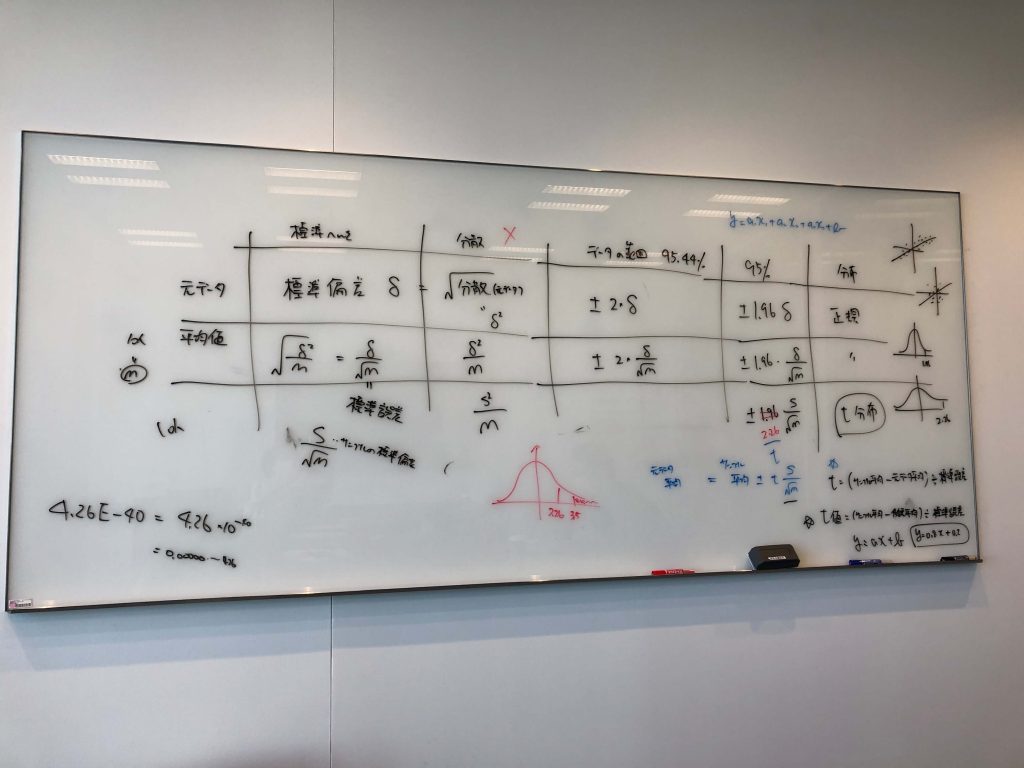
わたしのレベルは「δ」や「σ」のギリシャ文字を見て「これ何て読むんでしたっけ？」というところから質問しています。ちなみに読み方は「δ」＝デルタと「σ」＝シグマ。一般的には「母集団の標準偏差」＝「σ」、「標本の標準偏差」＝「ｓ」とすることが多いようです。

今回もほんとーーーに、動画制作までに最長時間を要し、ウラ紙とボールペンの消費量はさらに右肩上がりの創作現場です。

ふう～

チャンネル登録はこちら
YouTube公式チャンネル　NRIデータサイエンスラボ
https://www.youtube.com/channel/UCpy_3_wYutf5u0U4DdOziGQ

他の動画もぜひ♪

第１弾「クッキーレス時代の到来とは？」
第２弾「機械学習と統計学の関係とは？」
第３弾「今注目の因果推論とは？」
第４弾「ディープラーニング」
第５弾「ベイズ統計」
第６弾「コンテクストマッチ広告」
第７弾「ＧＰＴ－３」
第８弾「秘密計算」
第９弾「ベイジアンネットワーク」
第10弾「自動発注」
第11弾「回帰分析におけるｔ値とｐ値」